1/(1-x)の級数展開の数学 English German
船津好明
主要事項:1、定理、 2、定理の説明、 3、p,q が特別の場合、 4、定理の証明
5、aniの具体化、 6、1/(1+x)の展開、 7、応用例と経緯
数値計算例へ 1/(1±x)の種々の展開式へ
収束速度の検証 1/(1-x)の計算様式へ
1/(1+x)の計算様式へ
ここでは実数を取り扱う。
1、定理
任意の値 p,q(ただし p<q で、開区間 (p,q) が 1 を含まない。)をとれば、p<x<q なる x に対して、
1/(1-x)=an0+an1x+an2x2+...+annxn+rn ..........(1)
が成り立ち、任意の正数εに対し、|rn|<εとなる整数 n を見出すことができる。ani(i=0,1,2,...,n)は
p,q,n によって定まり、x を含まない。
 2、定理の説明
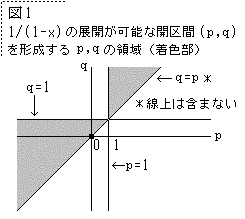
1/(1-x)を式(1)の形に展開できる (p,q) の領域は、図1に
示される。
1/(1-x) は 開区間の中の全ての x に対して、x のベキ級数
で近似でき、その誤差をいくらでも小さくすることができる。
x=-1 は特別の値ではない。1つの x の値に対する式(1)の右
辺のベキ級数は、1 を含まない開区間(p,q)の取り方によっ
て定まり、かつ、p,q は任意であるから、無限に多く存在す
る。展開式の近似の精度は p,q の値によって異なる。各 x
に対し、近似が最良となる級数が存在する。
式(1)において x を -x に置き換えると、1/(1+x) の展開
式の形になるが、その式の x の有効範囲は p<x<q ではな
く、-q<x<-p となる。p<x<q における 1/(1+x) の展開式
は、式(1)とは別の形になる。この場合 x=1 は特別の値では
ない。
以下におけるrnの値は、式ごとに異なるが、便宜rnで表す。
3、p,q が特別の場合
p=-1,q=1 のとき、即ち -1<x<1 のときは、ani=1(i=0,1,2,...,n)となり、
1/(1-x)=1+x+x2+...+xn+rn ..........(2)
となる。この式は既に知られている。-1<p=-q (-0.6<x<0.6など)の場合も式(2)の形になる。これ以外の
-1≦p<x<q≦1(0.8<x<1、-0.4<x<0.7 など)では、式(1)は式(2)と異なる形になる。-1<x<1の中の
x (≠0) に対しては、式(2)によるよりも近似のよい級数が存在する。
4、定理の証明
(前提)
任意の p,q の開区間(ただし p<qで、p=1 および q=1 は区間外とする。)の存在位置は、①1≦p、
②q≦1 に分けられる(境界共有)が、以下では ①1≦p の場合について式(1)を証明する。②の場合も
同様である。
2、定理の説明
1/(1-x)を式(1)の形に展開できる (p,q) の領域は、図1に
示される。
1/(1-x) は 開区間の中の全ての x に対して、x のベキ級数
で近似でき、その誤差をいくらでも小さくすることができる。
x=-1 は特別の値ではない。1つの x の値に対する式(1)の右
辺のベキ級数は、1 を含まない開区間(p,q)の取り方によっ
て定まり、かつ、p,q は任意であるから、無限に多く存在す
る。展開式の近似の精度は p,q の値によって異なる。各 x
に対し、近似が最良となる級数が存在する。
式(1)において x を -x に置き換えると、1/(1+x) の展開
式の形になるが、その式の x の有効範囲は p<x<q ではな
く、-q<x<-p となる。p<x<q における 1/(1+x) の展開式
は、式(1)とは別の形になる。この場合 x=1 は特別の値では
ない。
以下におけるrnの値は、式ごとに異なるが、便宜rnで表す。
3、p,q が特別の場合
p=-1,q=1 のとき、即ち -1<x<1 のときは、ani=1(i=0,1,2,...,n)となり、
1/(1-x)=1+x+x2+...+xn+rn ..........(2)
となる。この式は既に知られている。-1<p=-q (-0.6<x<0.6など)の場合も式(2)の形になる。これ以外の
-1≦p<x<q≦1(0.8<x<1、-0.4<x<0.7 など)では、式(1)は式(2)と異なる形になる。-1<x<1の中の
x (≠0) に対しては、式(2)によるよりも近似のよい級数が存在する。
4、定理の証明
(前提)
任意の p,q の開区間(ただし p<qで、p=1 および q=1 は区間外とする。)の存在位置は、①1≦p、
②q≦1 に分けられる(境界共有)が、以下では ①1≦p の場合について式(1)を証明する。②の場合も
同様である。
 (証明)
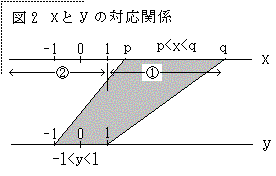
任意の正数を p,q(1≦p<q)とし、p<x<q なる x に
対し、もう一つの変数 y を立て、
y=(2x-q-p)/(q-p) ..........(3)
とおくと -1<y<1 となる。よって、
1/(1-y)=1+y+y2+...+yn+rn ..........(4)
が成り立つ。式(3)から
x={(q-p)y+(q+p)}/2 ..........(5)
となる。よって、
1/(1-x)=1/[1-{(q-p)y+(q+p)}/2]
={-2/(q+p-2)}{1+(q-p)y/(q+p-2)}-1 ..........(6)
となる。1≦p<q から y の係数は、0<(q-p)/(q+p-2),
(q-p)/(q+p-2)≦1 で、かつ、-1<y<1 であるから、|(q-p)y/(q+p-2)|<1 となる。よって式(6)は展開
可能で、
1/(1-x)={-2/(q+p-2)}[1-{(q-p)y/(q+p-2)}+{(q-p)y/(q+p-2)}2+...
+(-1)n{(q-p)y/(q+p-2)}n]+rn ..........(7)
となる。ここで右辺の n 次以下の y に式(3)を代入して変数を x に戻して、x のベキ級数に整理すれば、
式(1)の形になる。式(7)は収束級数であり、|rn|を任意の正数εより小さくすなるような n が存在すること
は明らかである。
なお、式(7)において変数を y から x に変更する場合、rn はそのままにしておく。式(7)のrn の中の
y を拾い集めることは正しくない。
5、ani の具体化
例として n=1,2,3,4 に対する ani を具体的に示す。
5.1 1次式
式(7)の級数において1次までとり、y に式(3)を代入して整理すると、
a10=-2{1+(q+p)/(q+p-2)}/(q+p-2), a11=4/(q+p-2)2 ..........(8)
となる。この a10, a11により、1次式は
1/(1-x)=a10+a11x+r1 ..........(9)
となる。
5.2 2次式
式(7)の級数において2次までとり、yに式(3)を代入して整理すると、
a20=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2]/(q+p-2),
a21=4{1+2(q+p)/(q+p-2)}/(q+p-2)2, a22=-8/(q+p-2)3 ..........(10)
となる。この a20, a21, a22により、2次式は
1/(1-x)=a20+a21x+a22x2+r2 ..........(11)
となる。
5.3 3次式
式(7)の級数において3次までとり、y に式(3)を代入して整理すると、
a30=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3]/(q+p-2),
a31=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2]/(q+p-2)2,
a32=-8{1+3(q+p)/(q+p-2)}/(q+p-2)3, a33=16/(q+p-2)4 ..........(12)
となる。これらにより、3次式は
1/(1-x)=a30+a31x+a32x2+a33x3+r3 ..........(13)
となる。
5.4 4次式
式(7)の級数において4次までとり、y に式(3)を代入して整理すると、
a40=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3+{(q+p)/(q+p-2)}4]/(q+p-2),
a41=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2+4{(q+p)/(q+p-2)}3]/(q+p-2)2,
a42=-8[1+3(q+p)/(q+p-2)+6{(q+p)/(q+p-2)}2]/(q+p-2)3,
a43=16{1+4(q+p)/(q+p-2)}/(q+p-2)4, a44=-32/(q+p-2)5 ..........(14)
となる。これらにより、4次式は
1/(1-x)=a40+a41x+a42x2+a43x3+a44x4+r4 ..........(15)
となる。
6、1/(1+x)の展開
任意の値 p,q(ただし、p<q で開区間 (p,q) が -1 を含まない。) をとれば p<x<q における x に
対して、
1/(1+x)=bn0+bn1x+bn2x2+...+bnnxn+rn ..........(16)
が成り立ち、任意の正数εに対し、|rn|<εとなる整数 n が存在する。特別の場合として、-p=q≦1 の
ときは 1/(1+x)=1-x+x2-x3+...+(-1)nxn+rn である。各bniを4次の係数まで示すと、以下の通りである。
b10=2{1+(q+p)/(q+p+2)}/(q+p+2), b11=-4/(q+p+2)2,
b20=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2]/(q+p+2),
b21=-4{1+2(q+p)/(q+p+2)}/(q+p+2)2, b22=8/(q+p+2)3,
b30=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3]/(q+p+2),
b31=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2]/(q+p+2)2,
b32=8{1+3(q+p)/(q+p+2)}/(q+p+2)3, b33=-16/(q+p+2)4,
b40=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3+{(q+p)/(q+p+2)}4]/(q+p+2),
b41=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2+4{(q+p)/(q+p+2)}3]/(q+p+2)2,
b42=8[1+3(q+p)/(q+p+2)+6{(q+p)/(q+p+2)}2]/(q+p+2)3,
b43=-16{1+4(q+p)/(q+p+2)}/(q+p+2)4, b44=32/(q+p+2)5 ..........(17)
7、応用例と経緯
統計学において応用した。変動範囲が有限の確率変数 X について、1/X の期待値を求めるに当たり、
定数 a(≠0)をとって、1/X=1/(a+X-a)=(1/a)[1/{1+(X-a)/a}] と変形し、右辺の展開に応用した。
理論により |(X-a)/a|<1 の条件は必要でない。著者はこの理論を1979年に発見し、その応用論文を
日本統計学会誌に寄稿したが、査読の結果、理論に間違いがあるとの判定で受け容れられなかった。
著者は判定を不服として、2つの論文をインドとアメリカに送った。そして2つとも間違いはないと
して認められ、次の通り学術誌に掲載された。
Y.Funatsu, A note 0n Koop's procedure to obtain the bias of the ratio estimate.
Sankhya: The Indian journal of statistics 1982, Volume 44, Series B, Pt.2, pp.219-222.
Y.Funatsu, A METHOD OF DERIVING VALID APPROXIMATE EXPRESSIONS FOR BIAS IN RATIO ESTIMATION.
Journal of Statistical Planning and Inference 6(1982)215-225, North Holland Publishing
Company.
これらにより著者は博士の学位を得て大学教授となった。 (以上)
(連絡先)
〒1870002 東京都小平市花小金井2-6-1 船津好明
Email funatsu@mvf.biglobe.ne.jp
本稿URL http://www.wwq.jp/
(証明)
任意の正数を p,q(1≦p<q)とし、p<x<q なる x に
対し、もう一つの変数 y を立て、
y=(2x-q-p)/(q-p) ..........(3)
とおくと -1<y<1 となる。よって、
1/(1-y)=1+y+y2+...+yn+rn ..........(4)
が成り立つ。式(3)から
x={(q-p)y+(q+p)}/2 ..........(5)
となる。よって、
1/(1-x)=1/[1-{(q-p)y+(q+p)}/2]
={-2/(q+p-2)}{1+(q-p)y/(q+p-2)}-1 ..........(6)
となる。1≦p<q から y の係数は、0<(q-p)/(q+p-2),
(q-p)/(q+p-2)≦1 で、かつ、-1<y<1 であるから、|(q-p)y/(q+p-2)|<1 となる。よって式(6)は展開
可能で、
1/(1-x)={-2/(q+p-2)}[1-{(q-p)y/(q+p-2)}+{(q-p)y/(q+p-2)}2+...
+(-1)n{(q-p)y/(q+p-2)}n]+rn ..........(7)
となる。ここで右辺の n 次以下の y に式(3)を代入して変数を x に戻して、x のベキ級数に整理すれば、
式(1)の形になる。式(7)は収束級数であり、|rn|を任意の正数εより小さくすなるような n が存在すること
は明らかである。
なお、式(7)において変数を y から x に変更する場合、rn はそのままにしておく。式(7)のrn の中の
y を拾い集めることは正しくない。
5、ani の具体化
例として n=1,2,3,4 に対する ani を具体的に示す。
5.1 1次式
式(7)の級数において1次までとり、y に式(3)を代入して整理すると、
a10=-2{1+(q+p)/(q+p-2)}/(q+p-2), a11=4/(q+p-2)2 ..........(8)
となる。この a10, a11により、1次式は
1/(1-x)=a10+a11x+r1 ..........(9)
となる。
5.2 2次式
式(7)の級数において2次までとり、yに式(3)を代入して整理すると、
a20=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2]/(q+p-2),
a21=4{1+2(q+p)/(q+p-2)}/(q+p-2)2, a22=-8/(q+p-2)3 ..........(10)
となる。この a20, a21, a22により、2次式は
1/(1-x)=a20+a21x+a22x2+r2 ..........(11)
となる。
5.3 3次式
式(7)の級数において3次までとり、y に式(3)を代入して整理すると、
a30=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3]/(q+p-2),
a31=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2]/(q+p-2)2,
a32=-8{1+3(q+p)/(q+p-2)}/(q+p-2)3, a33=16/(q+p-2)4 ..........(12)
となる。これらにより、3次式は
1/(1-x)=a30+a31x+a32x2+a33x3+r3 ..........(13)
となる。
5.4 4次式
式(7)の級数において4次までとり、y に式(3)を代入して整理すると、
a40=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3+{(q+p)/(q+p-2)}4]/(q+p-2),
a41=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2+4{(q+p)/(q+p-2)}3]/(q+p-2)2,
a42=-8[1+3(q+p)/(q+p-2)+6{(q+p)/(q+p-2)}2]/(q+p-2)3,
a43=16{1+4(q+p)/(q+p-2)}/(q+p-2)4, a44=-32/(q+p-2)5 ..........(14)
となる。これらにより、4次式は
1/(1-x)=a40+a41x+a42x2+a43x3+a44x4+r4 ..........(15)
となる。
6、1/(1+x)の展開
任意の値 p,q(ただし、p<q で開区間 (p,q) が -1 を含まない。) をとれば p<x<q における x に
対して、
1/(1+x)=bn0+bn1x+bn2x2+...+bnnxn+rn ..........(16)
が成り立ち、任意の正数εに対し、|rn|<εとなる整数 n が存在する。特別の場合として、-p=q≦1 の
ときは 1/(1+x)=1-x+x2-x3+...+(-1)nxn+rn である。各bniを4次の係数まで示すと、以下の通りである。
b10=2{1+(q+p)/(q+p+2)}/(q+p+2), b11=-4/(q+p+2)2,
b20=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2]/(q+p+2),
b21=-4{1+2(q+p)/(q+p+2)}/(q+p+2)2, b22=8/(q+p+2)3,
b30=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3]/(q+p+2),
b31=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2]/(q+p+2)2,
b32=8{1+3(q+p)/(q+p+2)}/(q+p+2)3, b33=-16/(q+p+2)4,
b40=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3+{(q+p)/(q+p+2)}4]/(q+p+2),
b41=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2+4{(q+p)/(q+p+2)}3]/(q+p+2)2,
b42=8[1+3(q+p)/(q+p+2)+6{(q+p)/(q+p+2)}2]/(q+p+2)3,
b43=-16{1+4(q+p)/(q+p+2)}/(q+p+2)4, b44=32/(q+p+2)5 ..........(17)
7、応用例と経緯
統計学において応用した。変動範囲が有限の確率変数 X について、1/X の期待値を求めるに当たり、
定数 a(≠0)をとって、1/X=1/(a+X-a)=(1/a)[1/{1+(X-a)/a}] と変形し、右辺の展開に応用した。
理論により |(X-a)/a|<1 の条件は必要でない。著者はこの理論を1979年に発見し、その応用論文を
日本統計学会誌に寄稿したが、査読の結果、理論に間違いがあるとの判定で受け容れられなかった。
著者は判定を不服として、2つの論文をインドとアメリカに送った。そして2つとも間違いはないと
して認められ、次の通り学術誌に掲載された。
Y.Funatsu, A note 0n Koop's procedure to obtain the bias of the ratio estimate.
Sankhya: The Indian journal of statistics 1982, Volume 44, Series B, Pt.2, pp.219-222.
Y.Funatsu, A METHOD OF DERIVING VALID APPROXIMATE EXPRESSIONS FOR BIAS IN RATIO ESTIMATION.
Journal of Statistical Planning and Inference 6(1982)215-225, North Holland Publishing
Company.
これらにより著者は博士の学位を得て大学教授となった。 (以上)
(連絡先)
〒1870002 東京都小平市花小金井2-6-1 船津好明
Email funatsu@mvf.biglobe.ne.jp
本稿URL http://www.wwq.jp/
 2、定理の説明
1/(1-x)を式(1)の形に展開できる (p,q) の領域は、図1に
示される。
1/(1-x) は 開区間の中の全ての x に対して、x のベキ級数
で近似でき、その誤差をいくらでも小さくすることができる。
x=-1 は特別の値ではない。1つの x の値に対する式(1)の右
辺のベキ級数は、1 を含まない開区間(p,q)の取り方によっ
て定まり、かつ、p,q は任意であるから、無限に多く存在す
る。展開式の近似の精度は p,q の値によって異なる。各 x
に対し、近似が最良となる級数が存在する。
式(1)において x を -x に置き換えると、1/(1+x) の展開
式の形になるが、その式の x の有効範囲は p<x<q ではな
く、-q<x<-p となる。p<x<q における 1/(1+x) の展開式
は、式(1)とは別の形になる。この場合 x=1 は特別の値では
ない。
以下におけるrnの値は、式ごとに異なるが、便宜rnで表す。
3、p,q が特別の場合
p=-1,q=1 のとき、即ち -1<x<1 のときは、ani=1(i=0,1,2,...,n)となり、
1/(1-x)=1+x+x2+...+xn+rn ..........(2)
となる。この式は既に知られている。-1<p=-q (-0.6<x<0.6など)の場合も式(2)の形になる。これ以外の
-1≦p<x<q≦1(0.8<x<1、-0.4<x<0.7 など)では、式(1)は式(2)と異なる形になる。-1<x<1の中の
x (≠0) に対しては、式(2)によるよりも近似のよい級数が存在する。
4、定理の証明
(前提)
任意の p,q の開区間(ただし p<qで、p=1 および q=1 は区間外とする。)の存在位置は、①1≦p、
②q≦1 に分けられる(境界共有)が、以下では ①1≦p の場合について式(1)を証明する。②の場合も
同様である。
2、定理の説明
1/(1-x)を式(1)の形に展開できる (p,q) の領域は、図1に
示される。
1/(1-x) は 開区間の中の全ての x に対して、x のベキ級数
で近似でき、その誤差をいくらでも小さくすることができる。
x=-1 は特別の値ではない。1つの x の値に対する式(1)の右
辺のベキ級数は、1 を含まない開区間(p,q)の取り方によっ
て定まり、かつ、p,q は任意であるから、無限に多く存在す
る。展開式の近似の精度は p,q の値によって異なる。各 x
に対し、近似が最良となる級数が存在する。
式(1)において x を -x に置き換えると、1/(1+x) の展開
式の形になるが、その式の x の有効範囲は p<x<q ではな
く、-q<x<-p となる。p<x<q における 1/(1+x) の展開式
は、式(1)とは別の形になる。この場合 x=1 は特別の値では
ない。
以下におけるrnの値は、式ごとに異なるが、便宜rnで表す。
3、p,q が特別の場合
p=-1,q=1 のとき、即ち -1<x<1 のときは、ani=1(i=0,1,2,...,n)となり、
1/(1-x)=1+x+x2+...+xn+rn ..........(2)
となる。この式は既に知られている。-1<p=-q (-0.6<x<0.6など)の場合も式(2)の形になる。これ以外の
-1≦p<x<q≦1(0.8<x<1、-0.4<x<0.7 など)では、式(1)は式(2)と異なる形になる。-1<x<1の中の
x (≠0) に対しては、式(2)によるよりも近似のよい級数が存在する。
4、定理の証明
(前提)
任意の p,q の開区間(ただし p<qで、p=1 および q=1 は区間外とする。)の存在位置は、①1≦p、
②q≦1 に分けられる(境界共有)が、以下では ①1≦p の場合について式(1)を証明する。②の場合も
同様である。
 (証明)
任意の正数を p,q(1≦p<q)とし、p<x<q なる x に
対し、もう一つの変数 y を立て、
y=(2x-q-p)/(q-p) ..........(3)
とおくと -1<y<1 となる。よって、
1/(1-y)=1+y+y2+...+yn+rn ..........(4)
が成り立つ。式(3)から
x={(q-p)y+(q+p)}/2 ..........(5)
となる。よって、
1/(1-x)=1/[1-{(q-p)y+(q+p)}/2]
={-2/(q+p-2)}{1+(q-p)y/(q+p-2)}-1 ..........(6)
となる。1≦p<q から y の係数は、0<(q-p)/(q+p-2),
(q-p)/(q+p-2)≦1 で、かつ、-1<y<1 であるから、|(q-p)y/(q+p-2)|<1 となる。よって式(6)は展開
可能で、
1/(1-x)={-2/(q+p-2)}[1-{(q-p)y/(q+p-2)}+{(q-p)y/(q+p-2)}2+...
+(-1)n{(q-p)y/(q+p-2)}n]+rn ..........(7)
となる。ここで右辺の n 次以下の y に式(3)を代入して変数を x に戻して、x のベキ級数に整理すれば、
式(1)の形になる。式(7)は収束級数であり、|rn|を任意の正数εより小さくすなるような n が存在すること
は明らかである。
なお、式(7)において変数を y から x に変更する場合、rn はそのままにしておく。式(7)のrn の中の
y を拾い集めることは正しくない。
5、ani の具体化
例として n=1,2,3,4 に対する ani を具体的に示す。
5.1 1次式
式(7)の級数において1次までとり、y に式(3)を代入して整理すると、
a10=-2{1+(q+p)/(q+p-2)}/(q+p-2), a11=4/(q+p-2)2 ..........(8)
となる。この a10, a11により、1次式は
1/(1-x)=a10+a11x+r1 ..........(9)
となる。
5.2 2次式
式(7)の級数において2次までとり、yに式(3)を代入して整理すると、
a20=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2]/(q+p-2),
a21=4{1+2(q+p)/(q+p-2)}/(q+p-2)2, a22=-8/(q+p-2)3 ..........(10)
となる。この a20, a21, a22により、2次式は
1/(1-x)=a20+a21x+a22x2+r2 ..........(11)
となる。
5.3 3次式
式(7)の級数において3次までとり、y に式(3)を代入して整理すると、
a30=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3]/(q+p-2),
a31=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2]/(q+p-2)2,
a32=-8{1+3(q+p)/(q+p-2)}/(q+p-2)3, a33=16/(q+p-2)4 ..........(12)
となる。これらにより、3次式は
1/(1-x)=a30+a31x+a32x2+a33x3+r3 ..........(13)
となる。
5.4 4次式
式(7)の級数において4次までとり、y に式(3)を代入して整理すると、
a40=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3+{(q+p)/(q+p-2)}4]/(q+p-2),
a41=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2+4{(q+p)/(q+p-2)}3]/(q+p-2)2,
a42=-8[1+3(q+p)/(q+p-2)+6{(q+p)/(q+p-2)}2]/(q+p-2)3,
a43=16{1+4(q+p)/(q+p-2)}/(q+p-2)4, a44=-32/(q+p-2)5 ..........(14)
となる。これらにより、4次式は
1/(1-x)=a40+a41x+a42x2+a43x3+a44x4+r4 ..........(15)
となる。
6、1/(1+x)の展開
任意の値 p,q(ただし、p<q で開区間 (p,q) が -1 を含まない。) をとれば p<x<q における x に
対して、
1/(1+x)=bn0+bn1x+bn2x2+...+bnnxn+rn ..........(16)
が成り立ち、任意の正数εに対し、|rn|<εとなる整数 n が存在する。特別の場合として、-p=q≦1 の
ときは 1/(1+x)=1-x+x2-x3+...+(-1)nxn+rn である。各bniを4次の係数まで示すと、以下の通りである。
b10=2{1+(q+p)/(q+p+2)}/(q+p+2), b11=-4/(q+p+2)2,
b20=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2]/(q+p+2),
b21=-4{1+2(q+p)/(q+p+2)}/(q+p+2)2, b22=8/(q+p+2)3,
b30=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3]/(q+p+2),
b31=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2]/(q+p+2)2,
b32=8{1+3(q+p)/(q+p+2)}/(q+p+2)3, b33=-16/(q+p+2)4,
b40=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3+{(q+p)/(q+p+2)}4]/(q+p+2),
b41=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2+4{(q+p)/(q+p+2)}3]/(q+p+2)2,
b42=8[1+3(q+p)/(q+p+2)+6{(q+p)/(q+p+2)}2]/(q+p+2)3,
b43=-16{1+4(q+p)/(q+p+2)}/(q+p+2)4, b44=32/(q+p+2)5 ..........(17)
7、応用例と経緯
統計学において応用した。変動範囲が有限の確率変数 X について、1/X の期待値を求めるに当たり、
定数 a(≠0)をとって、1/X=1/(a+X-a)=(1/a)[1/{1+(X-a)/a}] と変形し、右辺の展開に応用した。
理論により |(X-a)/a|<1 の条件は必要でない。著者はこの理論を1979年に発見し、その応用論文を
日本統計学会誌に寄稿したが、査読の結果、理論に間違いがあるとの判定で受け容れられなかった。
著者は判定を不服として、2つの論文をインドとアメリカに送った。そして2つとも間違いはないと
して認められ、次の通り学術誌に掲載された。
Y.Funatsu, A note 0n Koop's procedure to obtain the bias of the ratio estimate.
Sankhya: The Indian journal of statistics 1982, Volume 44, Series B, Pt.2, pp.219-222.
Y.Funatsu, A METHOD OF DERIVING VALID APPROXIMATE EXPRESSIONS FOR BIAS IN RATIO ESTIMATION.
Journal of Statistical Planning and Inference 6(1982)215-225, North Holland Publishing
Company.
これらにより著者は博士の学位を得て大学教授となった。 (以上)
(連絡先)
〒1870002 東京都小平市花小金井2-6-1 船津好明
Email funatsu@mvf.biglobe.ne.jp
本稿URL http://www.wwq.jp/
(証明)
任意の正数を p,q(1≦p<q)とし、p<x<q なる x に
対し、もう一つの変数 y を立て、
y=(2x-q-p)/(q-p) ..........(3)
とおくと -1<y<1 となる。よって、
1/(1-y)=1+y+y2+...+yn+rn ..........(4)
が成り立つ。式(3)から
x={(q-p)y+(q+p)}/2 ..........(5)
となる。よって、
1/(1-x)=1/[1-{(q-p)y+(q+p)}/2]
={-2/(q+p-2)}{1+(q-p)y/(q+p-2)}-1 ..........(6)
となる。1≦p<q から y の係数は、0<(q-p)/(q+p-2),
(q-p)/(q+p-2)≦1 で、かつ、-1<y<1 であるから、|(q-p)y/(q+p-2)|<1 となる。よって式(6)は展開
可能で、
1/(1-x)={-2/(q+p-2)}[1-{(q-p)y/(q+p-2)}+{(q-p)y/(q+p-2)}2+...
+(-1)n{(q-p)y/(q+p-2)}n]+rn ..........(7)
となる。ここで右辺の n 次以下の y に式(3)を代入して変数を x に戻して、x のベキ級数に整理すれば、
式(1)の形になる。式(7)は収束級数であり、|rn|を任意の正数εより小さくすなるような n が存在すること
は明らかである。
なお、式(7)において変数を y から x に変更する場合、rn はそのままにしておく。式(7)のrn の中の
y を拾い集めることは正しくない。
5、ani の具体化
例として n=1,2,3,4 に対する ani を具体的に示す。
5.1 1次式
式(7)の級数において1次までとり、y に式(3)を代入して整理すると、
a10=-2{1+(q+p)/(q+p-2)}/(q+p-2), a11=4/(q+p-2)2 ..........(8)
となる。この a10, a11により、1次式は
1/(1-x)=a10+a11x+r1 ..........(9)
となる。
5.2 2次式
式(7)の級数において2次までとり、yに式(3)を代入して整理すると、
a20=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2]/(q+p-2),
a21=4{1+2(q+p)/(q+p-2)}/(q+p-2)2, a22=-8/(q+p-2)3 ..........(10)
となる。この a20, a21, a22により、2次式は
1/(1-x)=a20+a21x+a22x2+r2 ..........(11)
となる。
5.3 3次式
式(7)の級数において3次までとり、y に式(3)を代入して整理すると、
a30=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3]/(q+p-2),
a31=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2]/(q+p-2)2,
a32=-8{1+3(q+p)/(q+p-2)}/(q+p-2)3, a33=16/(q+p-2)4 ..........(12)
となる。これらにより、3次式は
1/(1-x)=a30+a31x+a32x2+a33x3+r3 ..........(13)
となる。
5.4 4次式
式(7)の級数において4次までとり、y に式(3)を代入して整理すると、
a40=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3+{(q+p)/(q+p-2)}4]/(q+p-2),
a41=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2+4{(q+p)/(q+p-2)}3]/(q+p-2)2,
a42=-8[1+3(q+p)/(q+p-2)+6{(q+p)/(q+p-2)}2]/(q+p-2)3,
a43=16{1+4(q+p)/(q+p-2)}/(q+p-2)4, a44=-32/(q+p-2)5 ..........(14)
となる。これらにより、4次式は
1/(1-x)=a40+a41x+a42x2+a43x3+a44x4+r4 ..........(15)
となる。
6、1/(1+x)の展開
任意の値 p,q(ただし、p<q で開区間 (p,q) が -1 を含まない。) をとれば p<x<q における x に
対して、
1/(1+x)=bn0+bn1x+bn2x2+...+bnnxn+rn ..........(16)
が成り立ち、任意の正数εに対し、|rn|<εとなる整数 n が存在する。特別の場合として、-p=q≦1 の
ときは 1/(1+x)=1-x+x2-x3+...+(-1)nxn+rn である。各bniを4次の係数まで示すと、以下の通りである。
b10=2{1+(q+p)/(q+p+2)}/(q+p+2), b11=-4/(q+p+2)2,
b20=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2]/(q+p+2),
b21=-4{1+2(q+p)/(q+p+2)}/(q+p+2)2, b22=8/(q+p+2)3,
b30=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3]/(q+p+2),
b31=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2]/(q+p+2)2,
b32=8{1+3(q+p)/(q+p+2)}/(q+p+2)3, b33=-16/(q+p+2)4,
b40=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3+{(q+p)/(q+p+2)}4]/(q+p+2),
b41=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2+4{(q+p)/(q+p+2)}3]/(q+p+2)2,
b42=8[1+3(q+p)/(q+p+2)+6{(q+p)/(q+p+2)}2]/(q+p+2)3,
b43=-16{1+4(q+p)/(q+p+2)}/(q+p+2)4, b44=32/(q+p+2)5 ..........(17)
7、応用例と経緯
統計学において応用した。変動範囲が有限の確率変数 X について、1/X の期待値を求めるに当たり、
定数 a(≠0)をとって、1/X=1/(a+X-a)=(1/a)[1/{1+(X-a)/a}] と変形し、右辺の展開に応用した。
理論により |(X-a)/a|<1 の条件は必要でない。著者はこの理論を1979年に発見し、その応用論文を
日本統計学会誌に寄稿したが、査読の結果、理論に間違いがあるとの判定で受け容れられなかった。
著者は判定を不服として、2つの論文をインドとアメリカに送った。そして2つとも間違いはないと
して認められ、次の通り学術誌に掲載された。
Y.Funatsu, A note 0n Koop's procedure to obtain the bias of the ratio estimate.
Sankhya: The Indian journal of statistics 1982, Volume 44, Series B, Pt.2, pp.219-222.
Y.Funatsu, A METHOD OF DERIVING VALID APPROXIMATE EXPRESSIONS FOR BIAS IN RATIO ESTIMATION.
Journal of Statistical Planning and Inference 6(1982)215-225, North Holland Publishing
Company.
これらにより著者は博士の学位を得て大学教授となった。 (以上)
(連絡先)
〒1870002 東京都小平市花小金井2-6-1 船津好明
Email funatsu@mvf.biglobe.ne.jp
本稿URL http://www.wwq.jp/