A mathematics on expansion of 1/(1-x) German Japanese
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@Y. Funatsu
Contents 1.Theorem 2.Explanation 3.Special case of p and q 4.Proof of the theorem
5.Expressions of ani 6.Expansion of 1/(1+x) 7.Application and circumstance
@@@@@@@@@@@@@@@@@@ Numerical studies@Sample expressions of 1/(1}x)
Calculation form for 1/(1-x), 1/(1+x)
We treat real numbers here.
1. Theorem
@Let p,q (pq) be arbitrary two values. If the open interval (p,q) does not include 1, then we
have following expression for x in pxq.
1/(1-x)=an0+an1x+an2x2+...+annxn{rn@@..........(1)
where we can find n to be |rn|Γ, with a small positive value Γ, and aniii=0,1,2,...,njis
decided by p,q and n, irrespective of x.
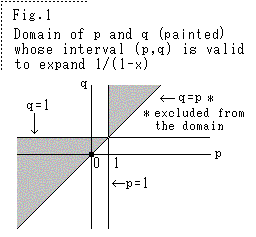 2. Explanation
Domain of p and q that makes (1) valid is shown in Fig.1.
Then 1/(1-x) can be approximated by power series of x in
the interval. The error can be as small as we wish. x=-1
is not special value. Since p and q are arbitrary, ani
varies for fixed x and there are numberless expressions
for fixed x. The precision of approximation varies by p,
q and n. For any x, there is the best series that makes
the error of approximation least.
If we replace x to -x in (1), the expression changes to
1/(1+x), then its valid interval is not (p,q), but (-q,-p).
The coefficients change too. x=1 is not special value
there.
In the expressions below, we write rn for simplicity,
although the value of which varies from expression to
expression.
3. Special case of p and q.
If p=-1 and q=1, that is, -1x1, we have ani=1 for i=0,1,2,...,n and
1/(1-x)=1+x+x2+...+xn+rn .......(2)
This is known formula. When -1p=-q (ex. -0.6x0.6), the expression is same as (2).
In other case (ex. 0.8x1,@-0.4x0.7), the expression is different from (2).
For x (0) in -1x1, there are series whose errors of approximation are smaller than (2).
4. Proof of the theorem
iPremisej
The interval (p,q) has two cases. One is @1
p and the other is Aq
1 (the border is
overlapping). We prove the case @1
p. The case Aq
1 will be
proved similarly.
2. Explanation
Domain of p and q that makes (1) valid is shown in Fig.1.
Then 1/(1-x) can be approximated by power series of x in
the interval. The error can be as small as we wish. x=-1
is not special value. Since p and q are arbitrary, ani
varies for fixed x and there are numberless expressions
for fixed x. The precision of approximation varies by p,
q and n. For any x, there is the best series that makes
the error of approximation least.
If we replace x to -x in (1), the expression changes to
1/(1+x), then its valid interval is not (p,q), but (-q,-p).
The coefficients change too. x=1 is not special value
there.
In the expressions below, we write rn for simplicity,
although the value of which varies from expression to
expression.
3. Special case of p and q.
If p=-1 and q=1, that is, -1x1, we have ani=1 for i=0,1,2,...,n and
1/(1-x)=1+x+x2+...+xn+rn .......(2)
This is known formula. When -1p=-q (ex. -0.6x0.6), the expression is same as (2).
In other case (ex. 0.8x1,@-0.4x0.7), the expression is different from (2).
For x (0) in -1x1, there are series whose errors of approximation are smaller than (2).
4. Proof of the theorem
iPremisej
The interval (p,q) has two cases. One is @1
p and the other is Aq
1 (the border is
overlapping). We prove the case @1
p. The case Aq
1 will be
proved similarly.
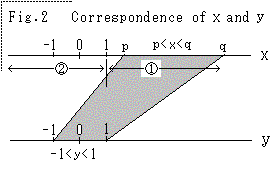 (Proof)
We can have another variable y for x in pxq, so
that we get
y=(2x-q-p)/(q-p) ........(3)
The corresponding interval of y is (-1,1), that is,
-1y1. The correspondence of x and y is shown in
Fig.2. Therefore we can have following expression
for y.
1/(1-y)=1+y+y2+...+yn+rn .......(4)
From (3) we have
x={(q-p)y+(q+p)}/2 ......(5)
and
1/(1-x)=1/[1-{(q-p)y+(q+p)}/2]
={-2/(q+p-2)}{1+(q-p)y/(q+p-2)}-1 .....(6)
Since 1
pq, the coefficient of y is positive and smaller than 1, that is,
0(q-p)/(q+p-2) and (q-p)/(q+p-2)
1.
And from -1y1, we have
|(q-p)y/(q+p-2)|1
Hence we can expand (6) as follows
1/(1-x)={-2/(q+p-2)}[1-{(q-p)y/(q+p-2)}+{(q-p)y/(q+p-2)}2+...
+(-1)n{(q-p)y/(q+p-2)}n]+rn .....(7)
Here we again replace y to x by (3) up to n-th power of y and put in order of power of x,
we finally obtain series (1). Since (4) and (7) are convergent when n¨, it is clear that
we can find n which satisfies |rn|Γ in (7) and (1).
In changing the variable y to x, we must leave rn as it is. It is wrong to collect y from rn
in (7).
5. Expressions of ani
For example, we show below ani for n=1,2,3,4
5.1 For n=1
We take terms in (7) up to first degree of y and replace y to x by (3).
Then
a10=-2{1+(q+p)/(q+p-2)}/(q+p-2), a11=4/(q+p-2)2@@@..........(8)
By these, we have
1/(1-x)=a10+a11x+r1 ..........(9)
5.2 For n=2
We take terms in (7) up to second degree of y and replace y to x by (3).
Then
a20=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2]/(q+p-2),
a21=4{1+2(q+p)/(q+p-2)}/(q+p-2)2, a22=-8/(q+p-2)3@@@ ..........(10)
By these, we have
1/(1-x)=a20+a21x+a22x2+r2 ..........(11)
5.3 For n=3
We take terms in (7) up to third degree of y and replace y to x by (3).
Then
a30=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3]/(q+p-2),
a31=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2]/(q+p-2)2,
a32=-8{1+3(q+p)/(q+p-2)}/(q+p-2)3, a33=16/(q+p-2)4@@@ ..........(12)
By these, we have
1/(1-x)=a30+a31x+a32x2+a33x3+r3 ..........(13)
5.4 For n=4
We take terms in (7) up to fourth degree of y and replace y to x by (3).
Then
a40=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3+{(q+p)/(q+p-2)}4]/(q+p-2),
a41=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2+4{(q+p)/(q+p-2)}3]/(q+p-2)2,
a42=-8[1+3(q+p)/(q+p-2)+6{(q+p)/(q+p-2)}2]/(q+p-2)3,
a43=16{1+4(q+p)/(q+p-2)}/(q+p-2)4, a44=-32/(q+p-2)5@@@@..........(14)
By these, we have
1/(1-x)=a40+a41x+a42x2+a43x3+a44x4+r4 ..........(15)
6. Expansion of 1/(1+x)
@Let p,q (pq) be arbitrary two values. If the interval (p,q) does not include -1, we have
following expression for x of pxq.
1/(1+x)=bn0+bn1x+bn2x2+...+bnnxn+rn ..........(16)
where we can find n to be |rn|Γ with a small positive value. bniii=0,1,2,...,njis decided
by p,q and n, irrespective of x. bni is generally different from ani.
As special case, if -p=q
1, we have
1/(1+x)=1-x+x2-...+(-1)nxn+rn
This formula is already known.
We show bni up to fourth degree below.
b10=2{1+(q+p)/(q+p+2)}/(q+p+2), b11=-4/(q+p+2)2,
b20=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2]/(q+p+2),
b21=-4{1+2(q+p)/(q+p+2)}/(q+p+2)2, b22=8/(q+p+2)3,
b30=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3]/(q+p+2),
b31=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2]/(q+p+2)2,
b32=8{1+3(q+p)/(q+p+2)}/(q+p+2)3, b33=-16/(q+p+2)4,
b40=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3+{(q+p)/(q+p+2)}4]/(q+p+2),
b41=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2+4{(q+p)/(q+p+2)}3]/(q+p+2)2,
b42=8[1+3(q+p)/(q+p+2)+6{(q+p)/(q+p+2)}2]/(q+p+2)3,
b43=-16{1+4(q+p)/(q+p+2)}/(q+p+2)4, b44=32/(q+p+2)5@@@..........(17)
7. Application and circumstance
It was applied to statistics. Let X be a random variable in a finite interval. When we seek the
expected value of 1/X, this theory is available. Taking fixed value a (0), we can write
as 1/X=1/(a+X-a)=(1/a)[1/{1+(X-a)/a}]. The theory does not require |(X-a)/a|1 for the expansion.
The author found this theory in 1979 and submitted a paper applying the theory to Japan
Statistical Society, but the referees rejected it by saying that the theory was wrong. The author
did not agree the judgement and sent two papers, one to India and another to U.S.A. They accepted
and appreciated the papers. The papers were issued by their publications like below.
Y.Funatsu, A note 0n Koop's procedure to obtain the bias of the ratio estimate.
Sankhya: The Indian journal of statistics 1982, Volume 44, Series B, Pt.2, pp.219-222.
Y.Funatsu, A METHOD OF DERIVING VALID APPROXIMATE EXPRESSIONS FOR BIAS IN RATIO ESTIMATION.
Journal of Statistical Planning and Inference 6(1982)215-225, North Holland Publishing
Company.
After these issues, the author got the degree of doctor and became a professor of university.
(Addresses)
Y. Funatsu
§1870002@Hanakoganei 2-6-1, kodairashi, Tokyo, Japan
Email funatsu@mvf.biglobe.ne.jp
(Proof)
We can have another variable y for x in pxq, so
that we get
y=(2x-q-p)/(q-p) ........(3)
The corresponding interval of y is (-1,1), that is,
-1y1. The correspondence of x and y is shown in
Fig.2. Therefore we can have following expression
for y.
1/(1-y)=1+y+y2+...+yn+rn .......(4)
From (3) we have
x={(q-p)y+(q+p)}/2 ......(5)
and
1/(1-x)=1/[1-{(q-p)y+(q+p)}/2]
={-2/(q+p-2)}{1+(q-p)y/(q+p-2)}-1 .....(6)
Since 1
pq, the coefficient of y is positive and smaller than 1, that is,
0(q-p)/(q+p-2) and (q-p)/(q+p-2)
1.
And from -1y1, we have
|(q-p)y/(q+p-2)|1
Hence we can expand (6) as follows
1/(1-x)={-2/(q+p-2)}[1-{(q-p)y/(q+p-2)}+{(q-p)y/(q+p-2)}2+...
+(-1)n{(q-p)y/(q+p-2)}n]+rn .....(7)
Here we again replace y to x by (3) up to n-th power of y and put in order of power of x,
we finally obtain series (1). Since (4) and (7) are convergent when n¨, it is clear that
we can find n which satisfies |rn|Γ in (7) and (1).
In changing the variable y to x, we must leave rn as it is. It is wrong to collect y from rn
in (7).
5. Expressions of ani
For example, we show below ani for n=1,2,3,4
5.1 For n=1
We take terms in (7) up to first degree of y and replace y to x by (3).
Then
a10=-2{1+(q+p)/(q+p-2)}/(q+p-2), a11=4/(q+p-2)2@@@..........(8)
By these, we have
1/(1-x)=a10+a11x+r1 ..........(9)
5.2 For n=2
We take terms in (7) up to second degree of y and replace y to x by (3).
Then
a20=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2]/(q+p-2),
a21=4{1+2(q+p)/(q+p-2)}/(q+p-2)2, a22=-8/(q+p-2)3@@@ ..........(10)
By these, we have
1/(1-x)=a20+a21x+a22x2+r2 ..........(11)
5.3 For n=3
We take terms in (7) up to third degree of y and replace y to x by (3).
Then
a30=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3]/(q+p-2),
a31=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2]/(q+p-2)2,
a32=-8{1+3(q+p)/(q+p-2)}/(q+p-2)3, a33=16/(q+p-2)4@@@ ..........(12)
By these, we have
1/(1-x)=a30+a31x+a32x2+a33x3+r3 ..........(13)
5.4 For n=4
We take terms in (7) up to fourth degree of y and replace y to x by (3).
Then
a40=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3+{(q+p)/(q+p-2)}4]/(q+p-2),
a41=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2+4{(q+p)/(q+p-2)}3]/(q+p-2)2,
a42=-8[1+3(q+p)/(q+p-2)+6{(q+p)/(q+p-2)}2]/(q+p-2)3,
a43=16{1+4(q+p)/(q+p-2)}/(q+p-2)4, a44=-32/(q+p-2)5@@@@..........(14)
By these, we have
1/(1-x)=a40+a41x+a42x2+a43x3+a44x4+r4 ..........(15)
6. Expansion of 1/(1+x)
@Let p,q (pq) be arbitrary two values. If the interval (p,q) does not include -1, we have
following expression for x of pxq.
1/(1+x)=bn0+bn1x+bn2x2+...+bnnxn+rn ..........(16)
where we can find n to be |rn|Γ with a small positive value. bniii=0,1,2,...,njis decided
by p,q and n, irrespective of x. bni is generally different from ani.
As special case, if -p=q
1, we have
1/(1+x)=1-x+x2-...+(-1)nxn+rn
This formula is already known.
We show bni up to fourth degree below.
b10=2{1+(q+p)/(q+p+2)}/(q+p+2), b11=-4/(q+p+2)2,
b20=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2]/(q+p+2),
b21=-4{1+2(q+p)/(q+p+2)}/(q+p+2)2, b22=8/(q+p+2)3,
b30=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3]/(q+p+2),
b31=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2]/(q+p+2)2,
b32=8{1+3(q+p)/(q+p+2)}/(q+p+2)3, b33=-16/(q+p+2)4,
b40=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3+{(q+p)/(q+p+2)}4]/(q+p+2),
b41=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2+4{(q+p)/(q+p+2)}3]/(q+p+2)2,
b42=8[1+3(q+p)/(q+p+2)+6{(q+p)/(q+p+2)}2]/(q+p+2)3,
b43=-16{1+4(q+p)/(q+p+2)}/(q+p+2)4, b44=32/(q+p+2)5@@@..........(17)
7. Application and circumstance
It was applied to statistics. Let X be a random variable in a finite interval. When we seek the
expected value of 1/X, this theory is available. Taking fixed value a (0), we can write
as 1/X=1/(a+X-a)=(1/a)[1/{1+(X-a)/a}]. The theory does not require |(X-a)/a|1 for the expansion.
The author found this theory in 1979 and submitted a paper applying the theory to Japan
Statistical Society, but the referees rejected it by saying that the theory was wrong. The author
did not agree the judgement and sent two papers, one to India and another to U.S.A. They accepted
and appreciated the papers. The papers were issued by their publications like below.
Y.Funatsu, A note 0n Koop's procedure to obtain the bias of the ratio estimate.
Sankhya: The Indian journal of statistics 1982, Volume 44, Series B, Pt.2, pp.219-222.
Y.Funatsu, A METHOD OF DERIVING VALID APPROXIMATE EXPRESSIONS FOR BIAS IN RATIO ESTIMATION.
Journal of Statistical Planning and Inference 6(1982)215-225, North Holland Publishing
Company.
After these issues, the author got the degree of doctor and became a professor of university.
(Addresses)
Y. Funatsu
§1870002@Hanakoganei 2-6-1, kodairashi, Tokyo, Japan
Email funatsu@mvf.biglobe.ne.jp
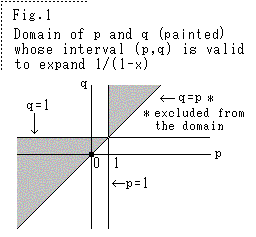 2. Explanation
Domain of p and q that makes (1) valid is shown in Fig.1.
Then 1/(1-x) can be approximated by power series of x in
the interval. The error can be as small as we wish. x=-1
is not special value. Since p and q are arbitrary, ani
varies for fixed x and there are numberless expressions
for fixed x. The precision of approximation varies by p,
q and n. For any x, there is the best series that makes
the error of approximation least.
If we replace x to -x in (1), the expression changes to
1/(1+x), then its valid interval is not (p,q), but (-q,-p).
The coefficients change too. x=1 is not special value
there.
In the expressions below, we write rn for simplicity,
although the value of which varies from expression to
expression.
3. Special case of p and q.
If p=-1 and q=1, that is, -1x1, we have ani=1 for i=0,1,2,...,n and
1/(1-x)=1+x+x2+...+xn+rn .......(2)
This is known formula. When -1p=-q (ex. -0.6x0.6), the expression is same as (2).
In other case (ex. 0.8x1,@-0.4x0.7), the expression is different from (2).
For x (0) in -1x1, there are series whose errors of approximation are smaller than (2).
4. Proof of the theorem
iPremisej
The interval (p,q) has two cases. One is @1
p and the other is Aq
1 (the border is
overlapping). We prove the case @1
p. The case Aq
1 will be
proved similarly.
2. Explanation
Domain of p and q that makes (1) valid is shown in Fig.1.
Then 1/(1-x) can be approximated by power series of x in
the interval. The error can be as small as we wish. x=-1
is not special value. Since p and q are arbitrary, ani
varies for fixed x and there are numberless expressions
for fixed x. The precision of approximation varies by p,
q and n. For any x, there is the best series that makes
the error of approximation least.
If we replace x to -x in (1), the expression changes to
1/(1+x), then its valid interval is not (p,q), but (-q,-p).
The coefficients change too. x=1 is not special value
there.
In the expressions below, we write rn for simplicity,
although the value of which varies from expression to
expression.
3. Special case of p and q.
If p=-1 and q=1, that is, -1x1, we have ani=1 for i=0,1,2,...,n and
1/(1-x)=1+x+x2+...+xn+rn .......(2)
This is known formula. When -1p=-q (ex. -0.6x0.6), the expression is same as (2).
In other case (ex. 0.8x1,@-0.4x0.7), the expression is different from (2).
For x (0) in -1x1, there are series whose errors of approximation are smaller than (2).
4. Proof of the theorem
iPremisej
The interval (p,q) has two cases. One is @1
p and the other is Aq
1 (the border is
overlapping). We prove the case @1
p. The case Aq
1 will be
proved similarly.
 (Proof)
We can have another variable y for x in pxq, so
that we get
y=(2x-q-p)/(q-p) ........(3)
The corresponding interval of y is (-1,1), that is,
-1y1. The correspondence of x and y is shown in
Fig.2. Therefore we can have following expression
for y.
1/(1-y)=1+y+y2+...+yn+rn .......(4)
From (3) we have
x={(q-p)y+(q+p)}/2 ......(5)
and
1/(1-x)=1/[1-{(q-p)y+(q+p)}/2]
={-2/(q+p-2)}{1+(q-p)y/(q+p-2)}-1 .....(6)
Since 1
pq, the coefficient of y is positive and smaller than 1, that is,
0(q-p)/(q+p-2) and (q-p)/(q+p-2)
1.
And from -1y1, we have
|(q-p)y/(q+p-2)|1
Hence we can expand (6) as follows
1/(1-x)={-2/(q+p-2)}[1-{(q-p)y/(q+p-2)}+{(q-p)y/(q+p-2)}2+...
+(-1)n{(q-p)y/(q+p-2)}n]+rn .....(7)
Here we again replace y to x by (3) up to n-th power of y and put in order of power of x,
we finally obtain series (1). Since (4) and (7) are convergent when n¨, it is clear that
we can find n which satisfies |rn|Γ in (7) and (1).
In changing the variable y to x, we must leave rn as it is. It is wrong to collect y from rn
in (7).
5. Expressions of ani
For example, we show below ani for n=1,2,3,4
5.1 For n=1
We take terms in (7) up to first degree of y and replace y to x by (3).
Then
a10=-2{1+(q+p)/(q+p-2)}/(q+p-2), a11=4/(q+p-2)2@@@..........(8)
By these, we have
1/(1-x)=a10+a11x+r1 ..........(9)
5.2 For n=2
We take terms in (7) up to second degree of y and replace y to x by (3).
Then
a20=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2]/(q+p-2),
a21=4{1+2(q+p)/(q+p-2)}/(q+p-2)2, a22=-8/(q+p-2)3@@@ ..........(10)
By these, we have
1/(1-x)=a20+a21x+a22x2+r2 ..........(11)
5.3 For n=3
We take terms in (7) up to third degree of y and replace y to x by (3).
Then
a30=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3]/(q+p-2),
a31=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2]/(q+p-2)2,
a32=-8{1+3(q+p)/(q+p-2)}/(q+p-2)3, a33=16/(q+p-2)4@@@ ..........(12)
By these, we have
1/(1-x)=a30+a31x+a32x2+a33x3+r3 ..........(13)
5.4 For n=4
We take terms in (7) up to fourth degree of y and replace y to x by (3).
Then
a40=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3+{(q+p)/(q+p-2)}4]/(q+p-2),
a41=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2+4{(q+p)/(q+p-2)}3]/(q+p-2)2,
a42=-8[1+3(q+p)/(q+p-2)+6{(q+p)/(q+p-2)}2]/(q+p-2)3,
a43=16{1+4(q+p)/(q+p-2)}/(q+p-2)4, a44=-32/(q+p-2)5@@@@..........(14)
By these, we have
1/(1-x)=a40+a41x+a42x2+a43x3+a44x4+r4 ..........(15)
6. Expansion of 1/(1+x)
@Let p,q (pq) be arbitrary two values. If the interval (p,q) does not include -1, we have
following expression for x of pxq.
1/(1+x)=bn0+bn1x+bn2x2+...+bnnxn+rn ..........(16)
where we can find n to be |rn|Γ with a small positive value. bniii=0,1,2,...,njis decided
by p,q and n, irrespective of x. bni is generally different from ani.
As special case, if -p=q
1, we have
1/(1+x)=1-x+x2-...+(-1)nxn+rn
This formula is already known.
We show bni up to fourth degree below.
b10=2{1+(q+p)/(q+p+2)}/(q+p+2), b11=-4/(q+p+2)2,
b20=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2]/(q+p+2),
b21=-4{1+2(q+p)/(q+p+2)}/(q+p+2)2, b22=8/(q+p+2)3,
b30=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3]/(q+p+2),
b31=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2]/(q+p+2)2,
b32=8{1+3(q+p)/(q+p+2)}/(q+p+2)3, b33=-16/(q+p+2)4,
b40=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3+{(q+p)/(q+p+2)}4]/(q+p+2),
b41=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2+4{(q+p)/(q+p+2)}3]/(q+p+2)2,
b42=8[1+3(q+p)/(q+p+2)+6{(q+p)/(q+p+2)}2]/(q+p+2)3,
b43=-16{1+4(q+p)/(q+p+2)}/(q+p+2)4, b44=32/(q+p+2)5@@@..........(17)
7. Application and circumstance
It was applied to statistics. Let X be a random variable in a finite interval. When we seek the
expected value of 1/X, this theory is available. Taking fixed value a (0), we can write
as 1/X=1/(a+X-a)=(1/a)[1/{1+(X-a)/a}]. The theory does not require |(X-a)/a|1 for the expansion.
The author found this theory in 1979 and submitted a paper applying the theory to Japan
Statistical Society, but the referees rejected it by saying that the theory was wrong. The author
did not agree the judgement and sent two papers, one to India and another to U.S.A. They accepted
and appreciated the papers. The papers were issued by their publications like below.
Y.Funatsu, A note 0n Koop's procedure to obtain the bias of the ratio estimate.
Sankhya: The Indian journal of statistics 1982, Volume 44, Series B, Pt.2, pp.219-222.
Y.Funatsu, A METHOD OF DERIVING VALID APPROXIMATE EXPRESSIONS FOR BIAS IN RATIO ESTIMATION.
Journal of Statistical Planning and Inference 6(1982)215-225, North Holland Publishing
Company.
After these issues, the author got the degree of doctor and became a professor of university.
(Addresses)
Y. Funatsu
§1870002@Hanakoganei 2-6-1, kodairashi, Tokyo, Japan
Email funatsu@mvf.biglobe.ne.jp
(Proof)
We can have another variable y for x in pxq, so
that we get
y=(2x-q-p)/(q-p) ........(3)
The corresponding interval of y is (-1,1), that is,
-1y1. The correspondence of x and y is shown in
Fig.2. Therefore we can have following expression
for y.
1/(1-y)=1+y+y2+...+yn+rn .......(4)
From (3) we have
x={(q-p)y+(q+p)}/2 ......(5)
and
1/(1-x)=1/[1-{(q-p)y+(q+p)}/2]
={-2/(q+p-2)}{1+(q-p)y/(q+p-2)}-1 .....(6)
Since 1
pq, the coefficient of y is positive and smaller than 1, that is,
0(q-p)/(q+p-2) and (q-p)/(q+p-2)
1.
And from -1y1, we have
|(q-p)y/(q+p-2)|1
Hence we can expand (6) as follows
1/(1-x)={-2/(q+p-2)}[1-{(q-p)y/(q+p-2)}+{(q-p)y/(q+p-2)}2+...
+(-1)n{(q-p)y/(q+p-2)}n]+rn .....(7)
Here we again replace y to x by (3) up to n-th power of y and put in order of power of x,
we finally obtain series (1). Since (4) and (7) are convergent when n¨, it is clear that
we can find n which satisfies |rn|Γ in (7) and (1).
In changing the variable y to x, we must leave rn as it is. It is wrong to collect y from rn
in (7).
5. Expressions of ani
For example, we show below ani for n=1,2,3,4
5.1 For n=1
We take terms in (7) up to first degree of y and replace y to x by (3).
Then
a10=-2{1+(q+p)/(q+p-2)}/(q+p-2), a11=4/(q+p-2)2@@@..........(8)
By these, we have
1/(1-x)=a10+a11x+r1 ..........(9)
5.2 For n=2
We take terms in (7) up to second degree of y and replace y to x by (3).
Then
a20=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2]/(q+p-2),
a21=4{1+2(q+p)/(q+p-2)}/(q+p-2)2, a22=-8/(q+p-2)3@@@ ..........(10)
By these, we have
1/(1-x)=a20+a21x+a22x2+r2 ..........(11)
5.3 For n=3
We take terms in (7) up to third degree of y and replace y to x by (3).
Then
a30=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3]/(q+p-2),
a31=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2]/(q+p-2)2,
a32=-8{1+3(q+p)/(q+p-2)}/(q+p-2)3, a33=16/(q+p-2)4@@@ ..........(12)
By these, we have
1/(1-x)=a30+a31x+a32x2+a33x3+r3 ..........(13)
5.4 For n=4
We take terms in (7) up to fourth degree of y and replace y to x by (3).
Then
a40=-2[1+(q+p)/(q+p-2)+{(q+p)/(q+p-2)}2+{(q+p)/(q+p-2)}3+{(q+p)/(q+p-2)}4]/(q+p-2),
a41=4[1+2(q+p)/(q+p-2)+3{(q+p)/(q+p-2)}2+4{(q+p)/(q+p-2)}3]/(q+p-2)2,
a42=-8[1+3(q+p)/(q+p-2)+6{(q+p)/(q+p-2)}2]/(q+p-2)3,
a43=16{1+4(q+p)/(q+p-2)}/(q+p-2)4, a44=-32/(q+p-2)5@@@@..........(14)
By these, we have
1/(1-x)=a40+a41x+a42x2+a43x3+a44x4+r4 ..........(15)
6. Expansion of 1/(1+x)
@Let p,q (pq) be arbitrary two values. If the interval (p,q) does not include -1, we have
following expression for x of pxq.
1/(1+x)=bn0+bn1x+bn2x2+...+bnnxn+rn ..........(16)
where we can find n to be |rn|Γ with a small positive value. bniii=0,1,2,...,njis decided
by p,q and n, irrespective of x. bni is generally different from ani.
As special case, if -p=q
1, we have
1/(1+x)=1-x+x2-...+(-1)nxn+rn
This formula is already known.
We show bni up to fourth degree below.
b10=2{1+(q+p)/(q+p+2)}/(q+p+2), b11=-4/(q+p+2)2,
b20=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2]/(q+p+2),
b21=-4{1+2(q+p)/(q+p+2)}/(q+p+2)2, b22=8/(q+p+2)3,
b30=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3]/(q+p+2),
b31=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2]/(q+p+2)2,
b32=8{1+3(q+p)/(q+p+2)}/(q+p+2)3, b33=-16/(q+p+2)4,
b40=2[1+(q+p)/(q+p+2)+{(q+p)/(q+p+2)}2+{(q+p)/(q+p+2)}3+{(q+p)/(q+p+2)}4]/(q+p+2),
b41=-4[1+2(q+p)/(q+p+2)+3{(q+p)/(q+p+2)}2+4{(q+p)/(q+p+2)}3]/(q+p+2)2,
b42=8[1+3(q+p)/(q+p+2)+6{(q+p)/(q+p+2)}2]/(q+p+2)3,
b43=-16{1+4(q+p)/(q+p+2)}/(q+p+2)4, b44=32/(q+p+2)5@@@..........(17)
7. Application and circumstance
It was applied to statistics. Let X be a random variable in a finite interval. When we seek the
expected value of 1/X, this theory is available. Taking fixed value a (0), we can write
as 1/X=1/(a+X-a)=(1/a)[1/{1+(X-a)/a}]. The theory does not require |(X-a)/a|1 for the expansion.
The author found this theory in 1979 and submitted a paper applying the theory to Japan
Statistical Society, but the referees rejected it by saying that the theory was wrong. The author
did not agree the judgement and sent two papers, one to India and another to U.S.A. They accepted
and appreciated the papers. The papers were issued by their publications like below.
Y.Funatsu, A note 0n Koop's procedure to obtain the bias of the ratio estimate.
Sankhya: The Indian journal of statistics 1982, Volume 44, Series B, Pt.2, pp.219-222.
Y.Funatsu, A METHOD OF DERIVING VALID APPROXIMATE EXPRESSIONS FOR BIAS IN RATIO ESTIMATION.
Journal of Statistical Planning and Inference 6(1982)215-225, North Holland Publishing
Company.
After these issues, the author got the degree of doctor and became a professor of university.
(Addresses)
Y. Funatsu
§1870002@Hanakoganei 2-6-1, kodairashi, Tokyo, Japan
Email funatsu@mvf.biglobe.ne.jp