信頼水準と信頼区間の関係
信頼水準1-αは、その意味から大きい方が望ましいようにみえますが、大きくし過ぎると、信頼区間が広がることとなり、
無意味になることがあります。
信頼水準の値を0.95前後とする例がよく見られますが、この値(0.95)が最適というわけではありません。
信頼水準は、信頼区間との関係で、程ほどの大きさが適切です。
信頼区間は、狭い方が望ましいようにみえますが、狭くし過ぎると、信頼水準が下がることとなり、無意味になることが
あります。
信頼区間の幅は、信頼水準との関係で、程ほどが適切です。
信頼区間は、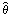 の確率分布の中で、任意に定めることができます。必ずしも連続区間(いわゆる
地続き)でなくても構いません。
信頼区間の幅を一定にして、
の確率分布の中で、任意に定めることができます。必ずしも連続区間(いわゆる
地続き)でなくても構いません。
信頼区間の幅を一定にして、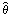 の確率分布の中で、信頼区間の位置を動かすと、信頼水準が
変化します。その中で信頼水準が一番高くなる信頼区間が、よい信頼区間といえます。
信頼水準を一定にして、
の確率分布の中で、信頼区間の位置を動かすと、信頼水準が
変化します。その中で信頼水準が一番高くなる信頼区間が、よい信頼区間といえます。
信頼水準を一定にして、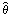 の確率分布の中で、信頼区間を色々な位置にとってみると、信頼
区間の幅が変化します。その中で最も狭いものがよい信頼区間です。
推定の精度が高いとは、信頼水準が高く、信頼区間の幅が狭い場合をいいます。
同じ母集団に対し、標本抽出の方式や標本規模を固定した場合、信頼水準を高めることと、信頼区間を狭めることは、
通常、同時にはできません。信頼水準を高めると、信頼区間が広がり、信頼区間を狭めると、信頼水準が低くなる傾向と
なります。よって、推定の一定の設計では、信頼水準と信頼区間の幅は、程ほどのバランスが適切となります。
の確率分布の中で、信頼区間を色々な位置にとってみると、信頼
区間の幅が変化します。その中で最も狭いものがよい信頼区間です。
推定の精度が高いとは、信頼水準が高く、信頼区間の幅が狭い場合をいいます。
同じ母集団に対し、標本抽出の方式や標本規模を固定した場合、信頼水準を高めることと、信頼区間を狭めることは、
通常、同時にはできません。信頼水準を高めると、信頼区間が広がり、信頼区間を狭めると、信頼水準が低くなる傾向と
なります。よって、推定の一定の設計では、信頼水準と信頼区間の幅は、程ほどのバランスが適切となります。





















目次 前頁(区間推定) 次頁(チェビシェフの不等式)
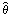 の確率分布の中で、任意に定めることができます。必ずしも連続区間(いわゆる
地続き)でなくても構いません。
信頼区間の幅を一定にして、
の確率分布の中で、任意に定めることができます。必ずしも連続区間(いわゆる
地続き)でなくても構いません。
信頼区間の幅を一定にして、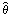 の確率分布の中で、信頼区間の位置を動かすと、信頼水準が
変化します。その中で信頼水準が一番高くなる信頼区間が、よい信頼区間といえます。
信頼水準を一定にして、
の確率分布の中で、信頼区間の位置を動かすと、信頼水準が
変化します。その中で信頼水準が一番高くなる信頼区間が、よい信頼区間といえます。
信頼水準を一定にして、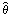 の確率分布の中で、信頼区間を色々な位置にとってみると、信頼
区間の幅が変化します。その中で最も狭いものがよい信頼区間です。
推定の精度が高いとは、信頼水準が高く、信頼区間の幅が狭い場合をいいます。
同じ母集団に対し、標本抽出の方式や標本規模を固定した場合、信頼水準を高めることと、信頼区間を狭めることは、
通常、同時にはできません。信頼水準を高めると、信頼区間が広がり、信頼区間を狭めると、信頼水準が低くなる傾向と
なります。よって、推定の一定の設計では、信頼水準と信頼区間の幅は、程ほどのバランスが適切となります。
の確率分布の中で、信頼区間を色々な位置にとってみると、信頼
区間の幅が変化します。その中で最も狭いものがよい信頼区間です。
推定の精度が高いとは、信頼水準が高く、信頼区間の幅が狭い場合をいいます。
同じ母集団に対し、標本抽出の方式や標本規模を固定した場合、信頼水準を高めることと、信頼区間を狭めることは、
通常、同時にはできません。信頼水準を高めると、信頼区間が広がり、信頼区間を狭めると、信頼水準が低くなる傾向と
なります。よって、推定の一定の設計では、信頼水準と信頼区間の幅は、程ほどのバランスが適切となります。




















