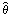チェビシェフの不等式

チェビシェフの不等式は、確率変数が、その期待値の周りの一定範囲内（外）に実現する確率を評価する式です。
確率変数を、その期待値をθ、標準偏差をσ(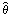)、任意の正数をkとするとき、チェビシェフの不等式は、
P(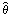｜-θ｜＜kσ(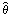))≧1-1/k2　　(1)
あるいは
P(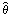｜-θ｜≧kσ(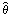))≦1-1/k2　 （2）
と表わされます。




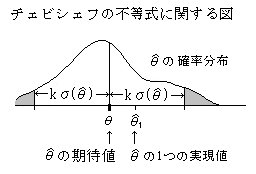
曲線下の全面積は1


曲線下の白い部分が式(1)の領域、　面積は1-1/k2以上


曲線下の灰色の部分が式(2)の領域、　面積は1-1/k2以下

チェビシェフの不等式は、期待値や分散が存在する任意の分布に対して成り立ちます。

チェビシェフの不等式(1)を簡単に言葉で言えば、例えば
「確率変数を多数回独立に実現させたとき、全実現値のほぼ3/4（75%）以上が期待値の周り標準偏差の2倍以内に入る。」
となります。

チェビシェフの不等式は、分布の形が定まると、不等号（カッコ外）を等号に変えることができます。
例えば、正規分布に対しては、k=2で、(1)式の左辺が約 0.95 となります。

チェビシェフの不等式は、区間推定の仕組みを理解するのに役立ちます。

チェビシェフの不等式：Chebyshev's　inequality