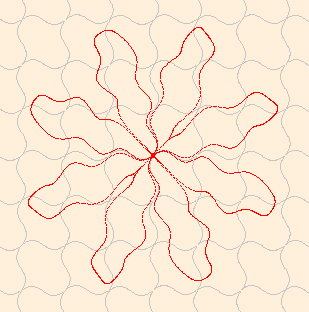
 左:関数座標系、 上:直交座標系
左:関数座標系、 上:直交座標系関数座標系と直交座標系の関係は 関数座標を (X,Y)、直交座標 を (W,Z) とすると、
W=X+a*Sin(b*Y), Z=Y+a*Sin(b*X) ここに、a は座標の揺れ幅の係数で、 0 に近いほど直交座標系に近くなります。
b は揺れの周波の係数で、大きいほど高周波になります。 左図では a=0.1, b=2 です。 目盛の単位 1 赤点は原点
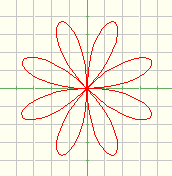
赤:X=3*Sin(4*T)*Cos(T) Y=3*Sin(4*T)*Sin(T) 0≦T<2π (T は媒介変数)
(どの桝目の目盛幅も1であることに注意)